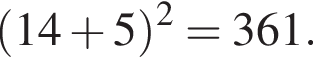На диаграмме показан средний балл участников 10 стран в тестировании учащихся 4-го класса, по естествознанию в 2007 году (по 1000-балльной шкале). По данным диаграммы найдите число стран, в которых средний балл участников выше, чем в Венгрии.
На рисунке жирными точками показан курс евро, установленный Центробанком РФ, во все рабочие дни в январе 2007 года. По горизонтали указываются числа месяца, по вертикали — цена евро в рублях. Для наглядности жирные точки на рисунке соединены линиями. Определите по рисунку наибольший курс евро в рублях в период с 16 по 27 января.
От дома до дачи можно доехать на автобусе, на электричке или на маршрутном такси. В таблице показано время, которое нужно затратить на каждый участок пути. Вычислите наименьшее время, которое потребуется на дорогу.
| Автобус | Электричка | Маршрутное такси |
|---|---|---|
| От дома до автобусной станции 20 мин | От дома до станции железной дороги —15 мин | От дома до остановки маршрутного такси — 25 мин |
| Автобус в пути 1 ч 55 мин | Электричка в пути — 1 ч 20 мин | Маршрутное такси в дороге 1 ч 30 мин |
| От остановки автобуса до дачи пешком 5 мин | От станции до дачи пешком 40 мин | От остановки маршрутного такси до дачи пешком 30 мин |
Пусть 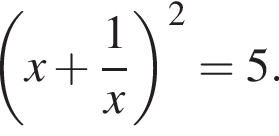 Значение выражения
Значение выражения 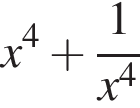 равно
равно
Дана арифметическая прогрессия 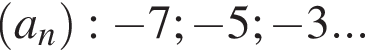 Найдите
Найдите ![]()
На доске записан ряд чисел 1; 2; 3; ...; 21. Какова вероятность того, что наугад выбранное число окажется простым?
В течение четверти оценки Вовы распределились следующим образом: двоек — 4, троек — 6, четвёрок — 7 и пятёрок — 5. Учитель предложил на выбор три способа выведения четвертной оценки.
Первый способ: оценка равна среднему арифметическому полученных оценок с последующим округлением до целого числа при необходимости. Второй: оценка равна моде всего ряда оценок. Третий способ: оценка равна медиане всего ряда полученных оценок с округлением до целого при необходимости. Какой способ является наиболее выгодным для Вовы?
Белка с орехом бежит со скоростью 3 м/с, а без ореха со скоростью 5 м/с Один орех в дупло она приносит за 16 минут. На каком расстоянии от дупла находятся орехи?
C трех земельных участков собрали 19,95 т урожая. Масса урожая, собранного с первого участка, относится к массе урожая, собранного со второго участка, как 5:9. С третьего участка собрали на 40% урожая больше, чем с первого. Сколько тонн урожая собрали с третьего участка?
Прямоугольный треугольник ABC, образован тремя полукругами. Вычислите периметр этого треугольника.
Какой наименьший угол составляет минутная и часовая стрелка в 16 часов 10 минут?
Oпределите площадь фигуры на рисунке, если площадь 1 клетки равна 1 см2.
Найдите площадь стены заводского здания изображенного на рисунке.
Паук и муха сидят на противоположных вершинах куба (см. рис.). Паук может ползти по ребру куба и по диагонали грани куба. Чему равно расстояние движения паука к мухе по короткому пути, если площадь поверхности куба равна 96 см2 (куб в подвешенном состоянии)?
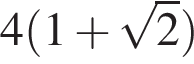 см
смКакое число необходимо вставить вместо вопросительного знака 12(256)4; 14(?)5?

 минут, на электричке
минут, на электричке  на маршрутном такси
на маршрутном такси 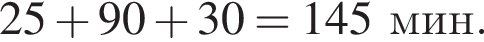 Значит, самым быстрым будет путь на электричке, 135 мин или
Значит, самым быстрым будет путь на электричке, 135 мин или 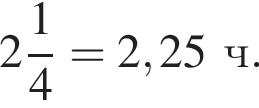
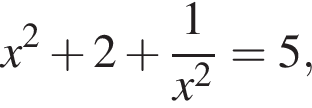 откуда
откуда 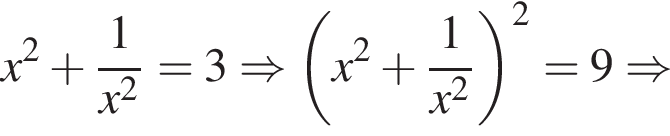
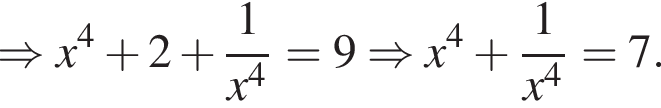
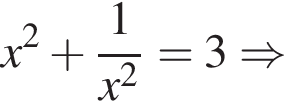
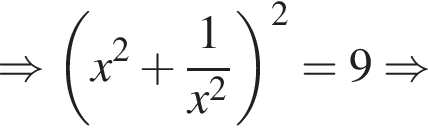
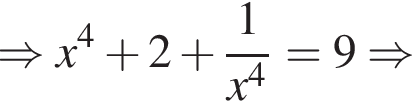
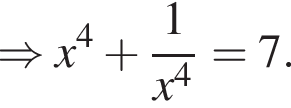
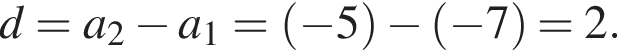
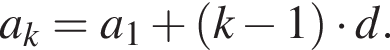
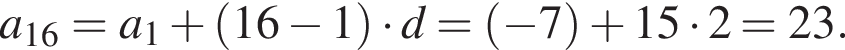
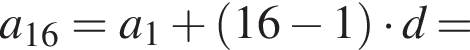
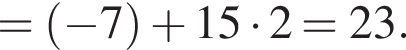
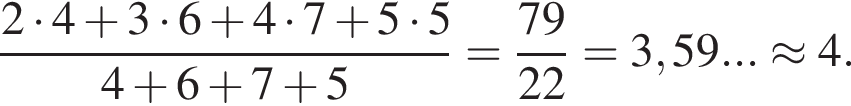
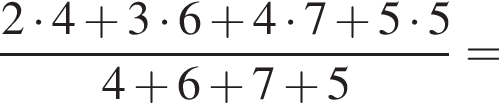
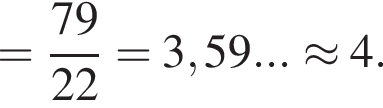
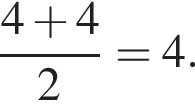
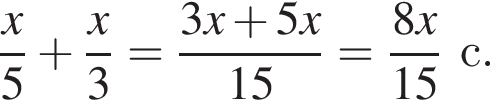
 секунд. Итак,
секунд. Итак, 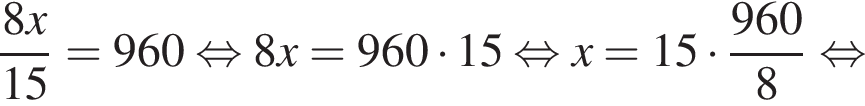
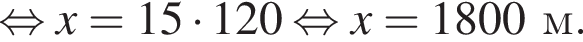
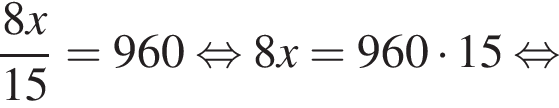
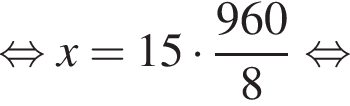
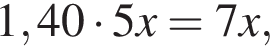 а со всех трех участков вместе
а со всех трех участков вместе 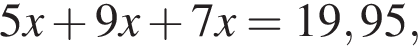 откуда
откуда 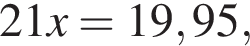 то есть
то есть 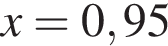 и
и 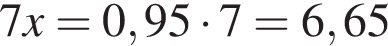 тонны.
тонны.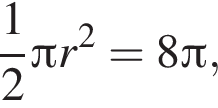 откуда
откуда  и
и 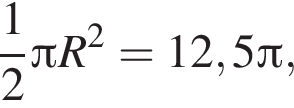 откуда
откуда  и
и 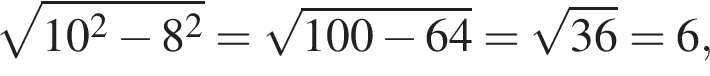

 градусов, а часовая пройдет
градусов, а часовая пройдет 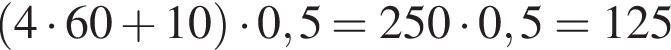
 градусов.
градусов. 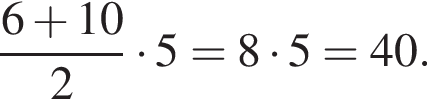
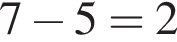 метрам, а длины оснований нам неизвестны, но вместе они составляют 18 метров. Если обозначить их за x, y, z метров, получим площадь
метрам, а длины оснований нам неизвестны, но вместе они составляют 18 метров. Если обозначить их за x, y, z метров, получим площадь 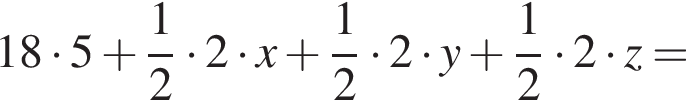

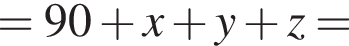
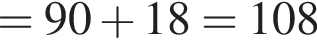

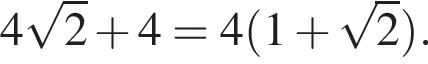
 можно вставить
можно вставить